MatheAsse

1. Einleitung

Extremwertaufgaben sind ein fester Bestandteil vom Abitur und haben auch in der echten Welt einige Anwendungen.

Stell dir vor, du bist auf einem Festival und möchtest deinen Platz rechteckig einzäunen. Dafür hast du 20m Zaun dabei und dein Platz grenzt an den Zaun vom Festivalgelände. Wie wird nun dein Bereich möglichst groß? Um diese Frage zu beantworten, müssen wir Extremwertaufgaben beherrschen.

Allgemein geht es bei Extremwertaufgaben also darum, etwas so groß wie möglich, so günstig wie möglich oder eben allgemein so extrem wie möglich (maximal oder minimal) zu bekommen. Außerdem gibt es immer eine zusätzliche Einschränkung, die erfüllt sein muss, wie zum Beispiel die Länge des Zauns einzuhalten.

Diese Aufgabenart ist immer folgendermaßen aufgebaut:

• Hauptbedingung: Was soll maximiert oder minimiert werden? Wir suchen nach einer allgemeinen Formel.
• Nebenbedingung: Welche Einschränkung muss beachtet werden? Wir suchen nach einer Formel mit der Zahl aus der Aufgabe.

Hier lernst du, Extremwertaufgaben zu erkennen, die Haupt- und Nebenbedingung aufzustellen und welche Schritte dich zuverlässig und schnell zur Lösung bringen.

Benötigtes Vorwissen:

Um in diesem Kapitel alles zu verstehen, solltest du am besten Folgendes verstanden haben und anwenden können:

• Textaufgaben verstehen und in Gleichungen umwandeln
• grundlegende Formeln für Flächeninhalte und Volumen kennen
• Funktionen sicher ableiten
• Extrempunkte von Funktionen finden
• Gleichungen sicher umstellen und lösen

Lass uns nun zuerst eine allgemeine Lösungsstrategie anschauen, dann rechnen wir ein typisches Beispiel detailliert durch und gucken uns noch häufige Fehler an. Am Ende kannst du dein Wissen mit Übungsaufgaben selbst testen.

2. Allgemeine Lösungsstrategie

Mit den folgenden Schritten kannst du jede Extremwertaufgabe systematisch angehen und sicher zur richtigen Lösung gelangen:

1. Aufgabenstellung verstehen (eventuell eine Skizze anfertigen, wenn es dir persönlich dabei hilft)
2. Hauptbedingung aufstellen (was möchten wir maximieren oder minimieren? Finde eine Formel dafür)
3. Nebenbedingung aufstellen (welche Einschränkung müssen wir beachten? Die Formel enthält die eine in der Aufgabe gegebene Zahl)
4. Nebenbedingung nach irgendeiner Variable umstellen (überlege, welche am einfachsten ist)
5. Erhaltene Formel in Hauptbedingung einsetzen (ersetze die Variable in der Hauptbedingung durch deine umgestellte Nebenbedingung) → diese Gleichung nennen wir “Zielfunktion”, die nur noch von einer Variablen abhängt
6. Sinnvollen Bereich der Variablen festlegen (welche Werte der Variablen ergeben im Kontext Sinn?)
7. Extremstellen und Art der Extrema bestimmen
   Wie mache ich das?

   • Zielfunktion ableiten (Erste Ableitung $f'(v)$ bilden).
   • Erste Ableitung Null setzen ($f'(v) = 0$).
   • Gleichung lösen, um mögliche Extremstellen $v_E$ zu bestimmen.
   • Zweite Ableitung der Zielfunktion bilden ($f''(v)$).
   • Art der Extrema bestimmen:
     • Setze die möglichen Extremstellen für $v$ in die zweite Ableitung $f''(v)$ ein:
     • Ist das Ergebnis $f''(v_E) > 0$, gehört der Wert zu einem lokalen Minimum.
     • Ist das Ergebnis $f''(v_E) < 0$, gehört der Wert zu einem lokalen Maximum.
     • Ist das Ergebnis $f''(v_E) = 0$, musst du das Vorzeichenwechselkriterium von $f'(v)$ nutzen:
       • Wechselt $f'(v)$ bei $v_E$ von $+$ nach $-$ $\rightarrow$ lokales Maximum.
       • Wechselt $f'(v)$ bei $v_E$ von $-$ nach $+$ $\rightarrow$ lokales Minimum.
   • Funktionswert der passenden Extremstelle in die Zielfunktion $f(v)$ einsetzen. Das gibt dir den Wert des lokalen Maximums oder Minimums.
8. Randwerte überprüfen (setze in der Zielfunktion die Randwerte für die Variable ein und überprüfe, ob du extremere Werte erhältst als bei den lokalen Extrema aus Schritt 7. Falls ja, dann ist der Randwert die gesuchte Lösung für das globale Extremum)
9. Gefundene Extremstelle in Nebenbedingung einsetzen (um übrige Variable(n) zu bestimmen)
10. Gefundene Extremstelle (und andere Variablen) in Hauptbedingung einsetzen (um die gesuchte Größe zu überprüfen)
11. Antwort formulieren

3. Beispielaufgabe: Das Festival-Camp

Aufgabenstellung: "Du bist auf einem Festival und möchtest mit deinen Freunden einen rechteckigen Bereich für eure Zelte abstecken. Ihr habt insgesamt 20 Meter mobilen Zaun dabei. Eine Seite eures Camps soll direkt am Bauzaun des Festivalgeländes liegen, sodass ihr für diese Seite keinen eigenen Zaun benötigt. Wie müsst ihr die Seitenlängen eures Camps wählen, damit die abgezäunte Fläche maximal wird, und wie groß ist diese maximale Fläche?"

Schritt 1: Aufgabenstellung verstehen

Gegeben:

• $20 \text{ m}$ langer Zaun
• Rechteckiges Camp
• Eine Seite am Bauzaun (benötigt keinen mobilen Zaun)

Gesucht:

• Seitenlängen $x$ und $y$ des Camps in $\text{m}$
• Flächeninhalt $A$ des Camps in $\text{m}^2$

Skizze:

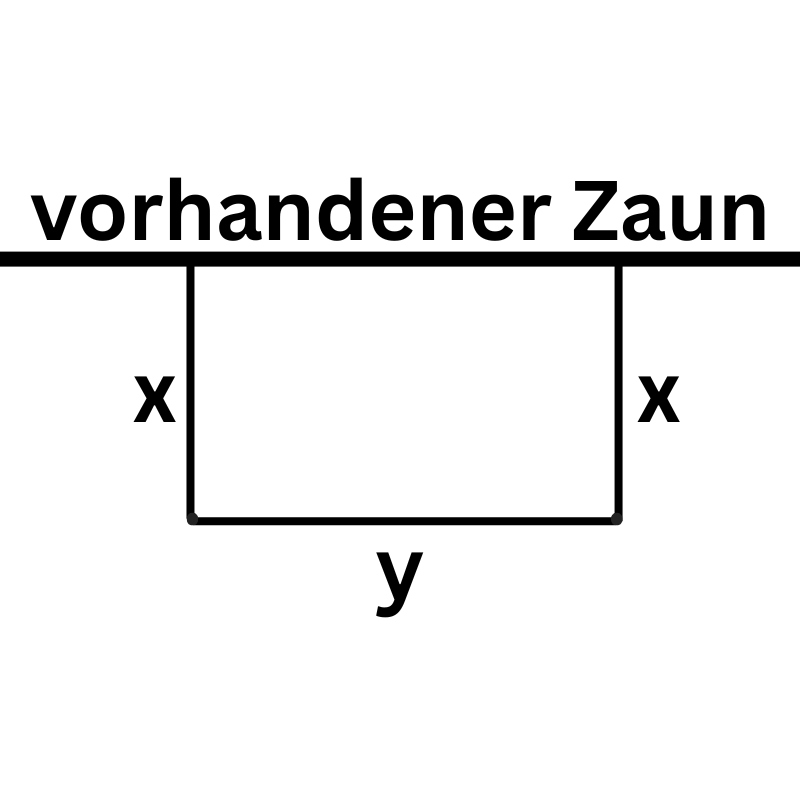
Wir definieren: $x$ ist die Länge der Seiten senkrecht zum Bauzaun, $y$ ist die Länge der Seite parallel zum Bauzaun.

Schritt 2: Hauptbedingung aufstellen

Wir möchten die Fläche $A$ maximieren, also brauchen wir eine Formel für die Fläche von einem Rechteck als Hauptbedingung.

Die allgemeine Formel für die Fläche eines Rechtecks ist $A = \text{Länge} \cdot \text{Breite}$. Mit unseren Variablen $x$ und $y$ ergibt das:

$$A = x \cdot y$$

Schritt 3: Nebenbedingung aufstellen

Die gegebene Einschränkung ist die Länge des Zauns mit $20 \text{ m}$.

Wir wollen zweimal die Seite $x$ (senkrecht zum Bauzaun) und einmal die Seite $y$ (parallel zum Bauzaun) einzäunen. Die vierte Seite des Rechtecks, die auch $y$ lang wäre, wird durch den vorhandenen Bauzaun abgedeckt.

Damit ergibt sich die Formel:

$$2x + y = 20$$

Schritt 4: Nebenbedingung umstellen

Wir überlegen uns zuerst, dass wir die Nebenbedingung lieber nach $y$ umstellen, da wir sonst Brüche erhalten:

$$2x + y = 20 \quad | -2x$$

$$y = 20 - 2x$$

Schritt 5: umgestellte Nebenbedingung in Hauptbedingung einsetzen, um die Zielfunktion zu bilden

Die Hauptbedingung war $A = x \cdot y$ und die umgestellte Nebenbedingung war $y = 20 - 2x$.

Ersetzen wir $y$ in der Hauptbedingung durch $(20 - 2x)$, ergibt sich:

$$A(x) = x \cdot (20 - 2x)$$

Ausmultiplizieren ergibt dann die Zielfunktion $A(x)$, die nur noch von $x$ abhängt:

$$A(x) = 20x - 2x^2$$

Diese Formel hängt nur noch von einer Variablen ab, somit haben wir unsere Zielfunktion korrekt aufgestellt.

Schritt 6: Sinnvollen Bereich der Variable festlegen

Da $x$ die Länge einer Seite des Zauns ist, muss $x$ positiv sein ($x > 0$).

Da wir nur $20 \text{m}$ Zaun haben und zweimal die Seite $x$ einzäunen müssen kann $x$ nicht länger als $10 \text{m}$ sein ($x < 10$).

Der sinnvolle Bereich für $x$ ist also $0 < x < 10$.

Schritt 7: Extrempunkte und Art der Extrema bestimmen

Erste Ableitung der Zielfunktion $A(x) = 20x - 2x^2$ bilden:

$$A'(x) = 20 - 4x$$

Erste Ableitung Null setzen ($A'(x) = 0$):

$$0 = 20 - 4x$$

Umstellen nach $x$:

$$0 = 20 - 4x \quad | +4x$$

$$4x = 20 \quad | :4$$

$$x = 5$$

Das bedeutet, dass $x=5$ unser Kandidat für eine Extremstelle ist.

Zweite Ableitung der Zielfunktion bilden:

$$A''(x) = -4$$

Beim Einsetzen des Kandidaten $x=5$ erhalten wir $A''(5) = -4$.

Da $A''(5) = -4 < 0$ ist, haben wir an der Stelle $x=5$ ein lokales Maximum gefunden (was auch laut Aufgabenstellung unser Ziel war).

Einsetzen von unserem Kandidaten $x=5$ in die Zielfunktion ergibt den Wert des lokalen Maximums:

$$A(5) = 20 \cdot 5 - 2 \cdot 5^2 = 100 - 2 \cdot 25 = 100 - 50 = 50$$

Schritt 8: Randwerte prüfen

Wir betrachten die Randwerte $0$ und $10$ und setzen sie für $x$ in die Zielfunktion $A(x) = 20x - 2x^2$ ein:

Für $x=0$ ergibt sich: $A(0) = 20 \cdot 0 - 2 \cdot 0^2 = 0$.

Für $x=10$ ergibt sich: $A(10) = 20 \cdot 10 - 2 \cdot 10^2 = 200 - 200 = 0$.

Unser lokales Maximum aus Schritt 7 hat den Wert $A(5) = 50$. Da $50$ der größte der drei Werte ist, liegt bei $x=5$ tatsächlich das globale Maximum.

Schritt 9: Übrige Variable bestimmen

Wir setzen unseren Wert für die Extremstelle $x=5 \text{ m}$ in unsere umgestellte Nebenbedingung $y=20-2x$ ein:

$$y = 20 - 2 \cdot 5 = 20 - 10 = 10$$

Schritt 10: Gesuchte Größe überprüfen (Kontrolle)

Zur Kontrolle setzen wir unseren Lösungswert $x=5 \text{ m}$ und die andere Variable $y=10 \text{ m}$ in die Hauptbedingung $A=x \cdot y$ ein:

$$A = 5 \text{ m} \cdot 10 \text{ m} = 50 \text{ m}^2$$

Das stimmt mit dem Wert aus Schritt 7 überein.

Schritt 11: Antwort formulieren

"Um mit $20 \text{ m}$ Zaun eine möglichst große rechteckige Camp-Fläche an dem vorhandenen Bauzaun abzugrenzen, müssen die beiden Seiten $x$ (senkrecht zum Bauzaun) jeweils $5 \text{ m}$ lang sein und die Seite $y$ (parallel zum Bauzaun) muss $10 \text{ m}$ lang sein. Die maximale Fläche des Camps beträgt dann $50 \text{ m}^2$."

4. Typische Fehler

Extremwertaufgaben haben einige häufige Fehlerquellen, auf die du achten solltest, um sie direkt zu vermeiden:

5. Übungsaufgaben

Übung 1: Das maximale Fenster

🧠 🧠 🧠 🧠 🧠

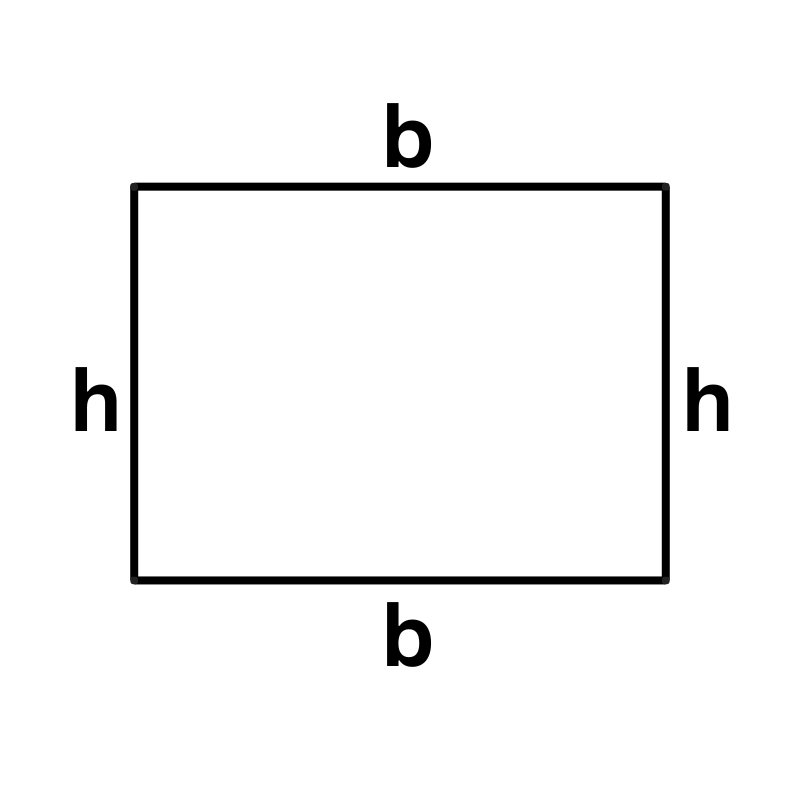
Aufgabenstellung: Ein rechteckiges Fenster soll eine möglichst große Fläche haben, damit möglichst viel Sonnenlicht in den Raum kommt. Der Umfang dieses Fensters soll $8 \text{ m}$ sein. Welche Seitenlängen muss das Fenster haben, damit seine Fläche maximal wird, und wie groß ist diese maximale Fläche?

Gib hier deine berechneten Endergebnisse ein:

Höhe h (in m):

Breite b (in m):

Maximale Fläche A (in m²):

Ergebnisse prüfen

Musterlösung:

Schritt 1: Aufgabenstellung verstehen

Gegeben:

• Umfang $U = 8 \text{ m}$
• Fensterform: rechteckig

Gesucht:

• Seitenlängen $h$ (Höhe) und $b$ (Breite) des Fensters in $\text{m}$
• Fläche $A$ des Fensters in $\text{m}^2$

Skizze:

Wir definieren: $b$ ist die Breite des Fensters, $h$ ist die Höhe des Fensters.

Schritt 2: Hauptbedingung aufstellen

Wir möchten die Fläche $A$ des rechteckigen Fensters maximieren.

Die allgemeine Formel für die Fläche eines Rechtecks ist $A = \text{Höhe} \cdot \text{Breite}$. Mit unseren Variablen $h$ und $b$ ergibt das:

$$A = h \cdot b$$

Schritt 3: Nebenbedingung aufstellen

Die gegebene Einschränkung ist der Umfang des Fensters mit $8 \text{ m}$.

Die allgemeine Formel für den Umfang eines Rechtecks ist $U = 2 \cdot \text{Höhe} + 2 \cdot \text{Breite}$.

Damit ergibt sich die Formel:

$$2h + 2b = 8$$

Schritt 4: Nebenbedingung umstellen

Da beide Variablen den selben Faktor vor sich haben, ist es egal, nach welcher wir umstellen möchten. Wir entscheiden uns für $b$:

$$2h + 2b = 8 \quad | :2$$

$$h + b = 4 \quad | -h$$

$$b = 4 - h$$

Schritt 5: umgestellte Nebenbedingung in Hauptbedingung einsetzen, um die Zielfunktion zu bilden

Die Hauptbedingung war $A = h \cdot b$ und die umgestellte Nebenbedingung war $b = 4 - h$.

Ersetzen wir $b$ in der Hauptbedingung durch $(4 - h)$, ergibt sich $A(h) = h \cdot (4 - h)$.

Ausmultiplizieren ergibt dann die Zielfunktion $A(h)$:

$$A(h) = 4h - h^2$$

Diese Formel hängt nur noch von einer Variablen ab, somit haben wir unsere Zielfunktion korrekt aufgestellt.

Schritt 6: Sinnvollen Bereich der Variable festlegen

Da $h$ die Höhe des Fensters ist, muss $h$ positiv sein ($h > 0$).

Da der Umfang $8 \text{m}$ sein soll und Höhe zweimal vorkommt kann $h$ also nicht größer als $4$ sein ($h < 4$).

Der sinnvolle Definitionsbereich für $h$ ist also $0 < h < 4$.

Schritt 7: Extrempunkte und Art der Extrema bestimmen

Erste Ableitung der Zielfunktion $A(h) = 4h - h^2$ bilden:

$$A'(h) = 4 - 2h$$

Erste Ableitung Null setzen ($A'(h) = 0$):

$$0 = 4 - 2h$$

Umstellen nach $h$:

$$0 = 4 - 2h \quad | +2h$$

$$2h = 4 \quad | :2$$

$$h = 2$$

Das bedeutet, dass $h=2$ unser Kandidat für eine Extremstelle ist.

Zweite Ableitung der Zielfunktion bilden:

$$A''(h) = -2$$

Beim Einsetzen des Kandidaten $h=2$ erhalten wir $A''(2) = -2$.

Da $A''(2) = -2 < 0$ ist, haben wir an der Stelle $h=2$ ein lokales Maximum gefunden.

Einsetzen von unserem Kandidaten $h=2$ in die Zielfunktion ergibt den Wert des lokalen Maximums:

$$A(2) = 4 \cdot 2 - 2^2 = 8 - 4 = 4$$

Schritt 8: Randwerte prüfen

Wir betrachten die Randwerte $0$ und $4$ und setzen sie in die Zielfunktion $A(h) = 4h - h^2$ ein:

Für $h=0$ ergibt sich: $A(0) = 4 \cdot 0 - 0^2 = 0$.

Für $h=4$ ergibt sich: $A(4) = 4 \cdot 4 - 4^2 = 16 - 16 = 0$.

Unser lokales Maximum aus Schritt 7 hat den Wert $A(2) = 4$. Da $4$ der größte der drei Werte ist, liegt bei $h=2$ tatsächlich das globale Maximum.

Schritt 9: Übrige Variable bestimmen

Wir setzen unseren Extremwert $h=2 \text{ m}$ in unsere umgestellte Nebenbedingung $b=4-h$ ein und erhalten:

$$b = 4 - 2 = 2$$

Schritt 10: Gesuchte Größe überprüfen (Kontrolle)

Zur Kontrolle setzen wir $h=2 \text{ m}$ und $b=2 \text{ m}$ in die Hauptbedingung $A=h \cdot b$ ein:

$$A = 2 \text{ m} \cdot 2 \text{ m} = 4 \text{ m}^2$$

Das stimmt mit dem Wert aus Schritt 7 überein.

Schritt 11: Antwort formulieren

"Um die Fläche des Fensters mit $8 \text{ m}$ Umfang zu maximieren, muss das Fenster eine Breite $b$ von $2 \text{ m}$ und eine Höhe $h$ von $2 \text{ m}$ haben. Damit ergibt sich ein Flächeninhalt von $4 \text{ m}^2$."

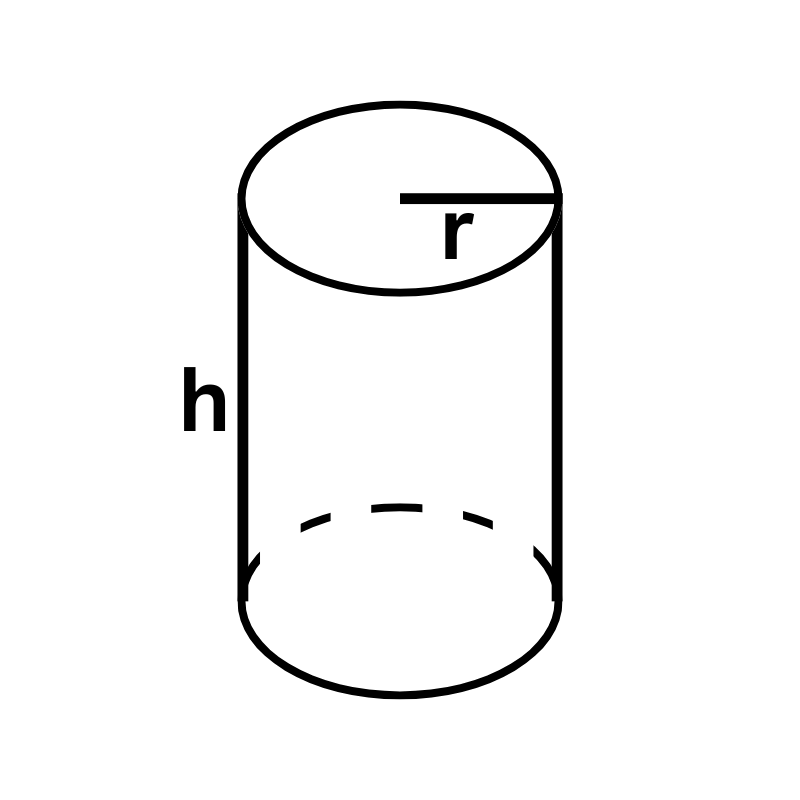
Übung 2: Die optimale Konservendose

🧠 🧠 🧠 🧠 🧠

Aufgabenstellung: Eine zylindrische Konservendose soll ein Volumen $V$ von $1000 \text{ cm}^3$ haben. Der Materialverbrauch für Boden, Deckel und Mantel der Dose soll dabei möglichst gering sein (d.h. die Oberfläche soll minimal sein). Welchen Radius $r$ und welche Höhe $h$ muss die Dose haben, um die Oberfläche $O$ zu minimieren, und wie groß ist diese minimale Oberfläche?

Gib hier deine berechneten Endergebnisse ein (runde auf eine Nachkommastelle, falls nötig):

Radius r (in cm):

Höhe h (in cm):

Minimale Oberfläche O (in cm²):

Ergebnisse prüfen

Musterlösung:

Schritt 1: Aufgabenstellung verstehen

Gegeben:

• Volumen $V = 1000 \text{ cm}^3$
• Dosenform: zylinderförmig (mit Boden und Deckel)

Gesucht:

• Radius $r$ der Dose in $\text{cm}$
• Höhe $h$ der Dose in $\text{cm}$
• Minimale Oberfläche $O_{min}$ der Dose in $\text{cm}^2$

Skizze:

Wir definieren: $r$ ist der Radius der Grundfläche der Dose, $h$ ist die Höhe der Dose.

Schritt 2: Hauptbedingung (HB) aufstellen

Wir möchten die Oberfläche $O$ der zylindrischen Konservendose minimieren.

Die Formel für die Oberfläche eines Zylinders (2 Grundflächen + Mantelfläche) ist:

$$O = 2\pi r^2 + 2\pi rh$$

Schritt 3: Nebenbedingung (NB) aufstellen

Die Einschränkung ist das Volumen der Dose mit $1000 \text{ cm}^3$.

Die Formel für das Volumen eines Zylinders ist $V = \pi r^2 h$.

Damit ergibt sich die Formel:

$$1000 = \pi r^2 h$$

Schritt 4: Nebenbedingung umstellen

Um keine Wurzel zu bekommen stellen wir die Nebenbedingung nach $h$ um:

$$1000 = \pi r^2 h \quad | :(\pi r^2)$$

$$h = \frac{1000}{\pi r^2}$$

Schritt 5: In Hauptbedingung einsetzen, um die Zielfunktion zu bilden

Wir setzen $h = \frac{1000}{\pi r^2}$ in die Hauptbedingung $O = 2\pi r^2 + 2\pi rh$ ein:

$$O(r) = 2\pi r^2 + 2\pi r \left(\frac{1000}{\pi r^2}\right)$$

Nach Vereinfachung (Kürzen von $\pi$ und einem $r$ im zweiten Teil) erhalten wir die Zielfunktion $O(r)$, die nur noch von $r$ abhängt:

$$O(r) = 2\pi r^2 + \frac{2000}{r}$$

Um das Ableiten zu erleichtern, können wir auch schreiben $O(r) = 2\pi r^2 + 2000r^{-1}$.

Schritt 6: Sinnvollen Bereich der Variable festlegen

Da $r$ der Radius der Dose ist, muss $r$ positiv sein ($r > 0$).

Für den maximalen Radius der Dose ergibt sich hier keine offensichtliche sinnvolle Grenze, wir lassen also die Obergrenze weg. Unser Bereich für $r$ ist also zwischen 0 und unendlich ($0 > r > \infty$).

Schritt 7: Extrempunkte und Art der Extrema bestimmen

Erste Ableitung der Zielfunktion $O(r) = 2\pi r^2 + 2000r^{-1}$ bilden:

$$O'(r) = 4\pi r - 2000r^{-2} = 4\pi r - \frac{2000}{r^2}$$

Erste Ableitung Null setzen ($O'(r) = 0$):

$$0 = 4\pi r - \frac{2000}{r^2} \quad | + \frac{2000}{r^2}$$

$$\frac{2000}{r^2} = 4\pi r \quad | \cdot r^2$$

$$2000 = 4\pi r^3 \quad | :(4\pi)$$

$$r^3 = \frac{2000}{4\pi} = \frac{500}{\pi}$$

$$r = \sqrt[3]{\frac{500}{\pi}} \approx 5,4 \text{ cm}$$

Dies ist unser Kandidat $(r_E)$ für eine Extremstelle.

Zweite Ableitung der Zielfunktion $O'(r) = 4\pi r - 2000r^{-2}$ bilden:

$$O''(r) = 4\pi + 4000r^{-3} = 4\pi + \frac{4000}{r^3}$$

Kandidaten für $r$ einsetzen:

$$O''(r_E) = 4\pi + \frac{4000}{500/\pi} = 4\pi + \frac{4000\pi}{500} = 4\pi + 8\pi = 12\pi$$

Da $O''(r_E) = 12\pi \approx 37,7 > 0$ ist, haben wir an der Stelle $r_E$ ein lokales Minimum gefunden.

Wert des lokalen Minimums berechnen: Wir setzen $\sqrt[3]{\frac{500}{\pi}}$ für $r$ in $O(r) = 2\pi r^2 + \frac{2000}{r}$ ein.

$$O(r_E) = 2\pi {\sqrt[3]{\frac{500}{\pi}}}^2 + \frac{2000}{\sqrt[3]{\frac{500}{\pi}}} \approx 553,6 \text{ cm}^2$$

Schritt 8: Randwerte prüfen

Unser sinnvoller Bereich für $r$ ist $(0, \infty)$. Wir untersuchen also das Verhalten der Zielfunktion $O(r) = 2\pi r^2 + \frac{2000}{r}$ an den Rändern dieses Bereichs:

• Für $r \rightarrow 0$: Der Term $2\pi r^2 \rightarrow 0$, aber der Term $\frac{2000}{r} \rightarrow +\infty$. Also ergibt sich insgesamt $\lim_{r\to0} O(r) = +\infty$.
• Für $r \rightarrow \infty$: Der Term $2\pi r^2 \rightarrow +\infty$, während der Term $\frac{2000}{r} \rightarrow 0$. Also ergibt sich insgesamt $\lim_{r\to\infty} O(r) = +\infty$.

Da die Funktion an beiden "Rändern" des sinnvollen Bereichs gegen Unendlich geht und wir bei $r_E \approx 5,4 \text{ cm}$ ein lokales Minimum mit ($O(r_E) \approx 553,6 \text{ cm}^2$) gefunden haben, ist dieses lokale Minimum auch die gesuchte Lösung.

Schritt 9: Übrige Variable bestimmen

Wir setzen $r_E = \sqrt[3]{\frac{500}{\pi}} \text{ cm}$ in $h = \frac{1000}{\pi r_E^2}$ ein:

$$h_E = \frac{1000}{\pi \sqrt[3]{\frac{500}{\pi}}^2} \approx 10,8$$

Schritt 10: Gesuchte Größe überprüfen (Kontrolle)

Zur Kontrolle setzen wir $r_E \approx 5,4 \text{ cm}$ und $h_E \approx 10,8 \text{ cm}$ in die Hauptbedingung $O = 2\pi r^2 + 2\pi rh$ ein:

$$O \approx 2\pi (5,4)^2 + 2\pi (5,4)(10,8)$$

$$O \approx 2\pi (29,3) + 2\pi (58,7) \approx 184,6 + 369 \approx 553,6 \text{ cm}^2$$

Dies stimmt mit dem Wert aus Schritt 7 überein.

Schritt 11: Antwort formulieren

"Um die Oberfläche der Konservendose mit einem Volumen von $1000 \text{ cm}^3$ zu minimieren, muss die Dose einen Radius $r$ von ca. $5,4 \text{ cm}$ und eine Höhe $h$ von ca. $10,8 \text{ cm}$ haben. Die minimale Oberfläche beträgt dann ca. $553,6 \text{ cm}^2$."